Deep Learning Notes


本文整理深度学习学习过程中相关的笔记，包括神经网络最基本的几个点（激活函数、参数初始化、防止过拟合），常见的网络结构（FC、CNN、RNN），以及一些常见的问题、 Tricks、注意事项等。


目录

Deep Learning & Machine Learning

  • 最表层的关系，deep learing 是机器学习一种，是具有更多层数的神经网络

  • 传统的机器学习工程中需要花费很多精力对数据的 feature 进行抽取(feature 的抽取很大程度影响最后的效果)，deep learning 则是可以输入 raw input(比如图像，语音，自然语言等)通过网络学习自动挖掘数据的 feature，即对数据进行 representation。(挖掘数据的内部结构)

  • 从数据量的角度，深度学习需要比传统机器学习算法更多的数据量才能有效果

DL 的核心思想:
选择神经网络作为函数拟合器，选择一个恰当的损失函数，通过梯度下降优化网络参数达到降低损失的效果

Supervised Learning 目标:
获取一个能在没见过的数据上表现良好(预测正确率高)的函数 -> 最小化训练数据上的 [预测误差+正则误差]


Activation Functions

神经网络中的激活函数本质上就是在线性计算中加入非线性的成分，使神经网络能够拟合复杂函数。

  • Sigmoid

Sigmoid 将一个 real-value 压缩到[0,1]之间，很小的负数接近与 0，很大的正数接近与 1。其计算公式如下

$$ F(z)=\frac{1}{(1+\exp(-z))} $$ $$ F^{'}=F(z)(1-F(z)) $$

Sigmoid 激活函数有两个主要的缺点:

  1. 容易饱和使得梯度消失，当 hidden layer 的输出是很小的负数或很大的正数时，Sigmoid 的导数接近与 0，由于参数的梯度需要乘上 Sigmoid 的导数，因此梯度会变得很小，阻止了梯度信号传递.
  2. Sigmoid 的输出不是零中心的，由于 Sigmoid 输出总为正，因此当输入全为正(负)时，所有参数梯度都为正(负)，使得学习呈现 Z 字形。
  • Tanh（Hyperbolic Tangent）

Tanh 和 Sigmoid 类似，将实值输入挤压到 [-1,1] 区间内，同样存在饱和导致梯度消失的问题，不过比 Sigmoid 好的地方是 Tanh 的输出是零中心的。

$$ F(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}}$$ $$ F^{'}=1-F(z)^2 $$
  • ReLU （Rectified Linear Unit）

ReLU 激活函数对非正输入直接输出 0，对于正输入直接输出原值，是神经网络中最常用的一种激活函数，其公式及其导数如下

$$ F(z)=\max(0,z) $$ $$ F(z)=\{ \begin{matrix} 1 \quad z>0\\ 0 \quad z<0 \end{matrix} $$

优点

  1. 相比 Sigmoid 和 Tanh，在使用随机梯度下降的时候能够更快的收敛。
  2. 相比 Sigmoid，Tanh 等需要指数计算，ReLU 计算速度更快.
  3. 没有饱和问题，不会出先梯度消失的情况

缺点: 可能会出现 dying ReLU 问题。某次更新梯度过大时，会使参数空间转移到某种状态，在这种状态下所有输入数据通过 ReLU 后都为 0，流过神经元的梯度都是 0，参数永远得不到更新，因此是一种不可逆的神经元死亡。

  • Leaky ReLU
$$ F(z)=\{ \begin{matrix} z \quad z>0\\ \alpha z \quad z<0 \end{matrix} $$

其中 \(\alpha\) 是一个很小的常量，主要是给负输入一个很小的梯度，解决死亡的问题。

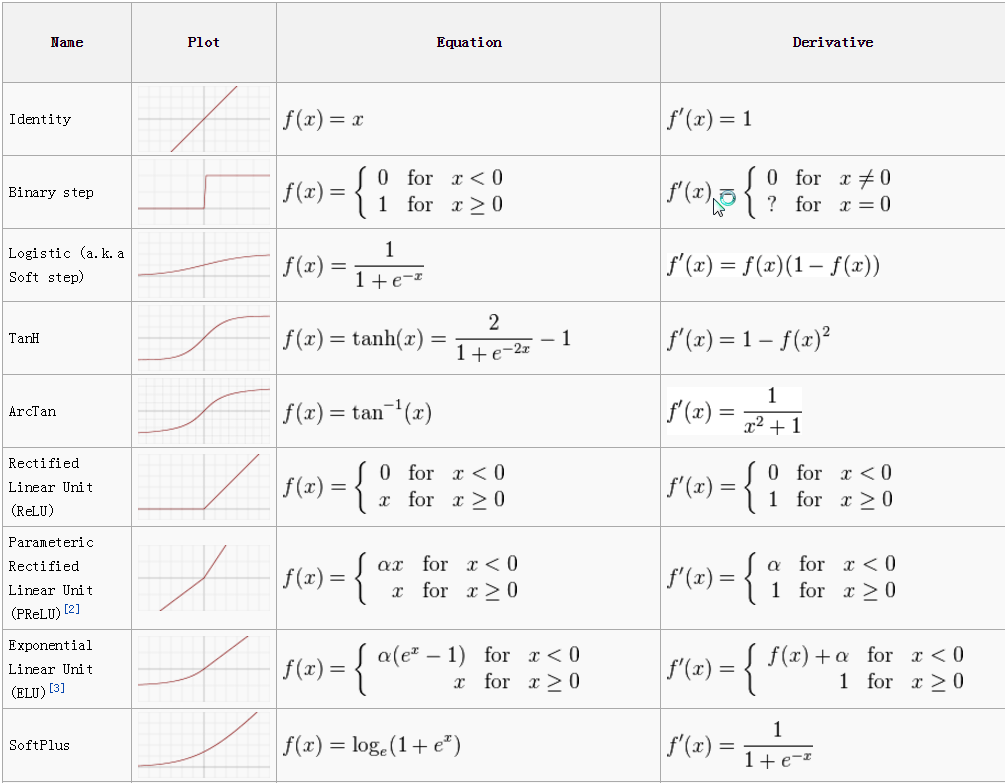
  • 各种激活函数及其导数总结如下图
activation_fn1
activation_fn2


Parameter Initialization

神经网络中包含大量的参数，参数的初始化位置对于模型最终的性能有较大的影响。以下介绍几种不同的参数初始化方法。

  • 全零初始化（WRONG！）

使用全零初始化时会导致网络中每个神经元都计算得到同样的输出，在反向传播的额时候都得到同样的梯度，进而进行同样的参数更新。这种对称性使网络没办法学到任何东西。

  • 小随机数初始化

权重的初始值应该非常接近于 0 但不等于 0 以此打破对称性。一种实现方法是从一个高斯分布中随机采样得到参数。示例代码如下

W = np.random.randn(in_dim, out_dim) * 0.01

小随机数在深层神经网络中可能会出现问题，因为如果权重值很小，在反向传播的时候的梯度也会很小（因为梯度和权重值成比例），因此会减小反向传播中的梯度信号。

  • 校正方差

在上面的小随机数初始化方法中，所有不同的参数都简单地使用的 0.01 进行缩放（而没有考虑 W 的维度。由于不同网络层的 W 维度不同，可能导致各层经过 W 后的计算值的方差不一致，因此考虑输入参数 W 的维度对随机数进行缩放。以下代码展示了三种常用的初始化方法。

# He et al. (Widely used with ReLU. Best practice.)
W = np.random.randn(in_dim, out_dim) * np.sqrt(2 / in_dim)
# Xavier (Used with Sigmoid and Tanh)
W = np.random.randn(in_dim, out_dim) * np.sqrt(1 / in_dim)
# Other
W = np.random.randn(in_dim, out_dim) * np.sqrt(2 / (in_dim + out_dim))


Regularization

  • L2 正则化

    最常用的一种正则化方法。在损失函数中加入网络权值的惩罚项 \(\frac{\lambda}{2} \left\| w \right\|^{2}\)。其中 \(\lambda\) 为正则系数。 L2 正则对大数值的权重进行惩罚，使权重更加分散，这样有利于抑制模型过于依赖少数特征，使其可以更好地使用数据的多个特征。

  • L1 正则化

    在损失函数中加入惩罚项 \(\lambda \left\|w\right\|^1\)。L1 正则倾向于使参数变得稀疏（既使参数变为 0）。在实践中不如 L2 正则应用广泛。L1 正则也可以与 L2 正则结合起来：\(\lambda_{1} \left\|w\right\|^1+\frac{\lambda_{2}}{2} \left\|w\right\|^2\)。其中 \(\left\|w\right\|^k=\sqrt[k]{\sum w^k}\)

  • Dropout

    Dropout 是一种简单有效的正则化方法。其实现方法是让网络神经元以一定概率 p 失活（权重设为 0）。Dropout 可以理解为对完整的神经网络抽出一个子集，每次的训练只更新抽出的子网的参数（让完整的网络不要太聪明，可以避免过拟合)。也包含了 Ensemble Learning 的思想，集成多个比较小的子网络的学习。同时由于训练时对神经元随机失活，也相当于对网络层随机注入噪声扰动，增强模型泛化能力。

    测试的时候不再使用 Dropout，但由于在训练时进行了 Dropout，使得网络的输出期望比不使用 Dropout 小，因此测试时要对网络的输出进行数值调整（乘以 p）
    实践中采用 Inverse Dropout，即在训练进行 Dropout 时就对数值进行调整(除以 p)，这样在预测时就无需再对网络输出进行调整。

    同时实践中也有对不同的网络层采取不同的存活概率 p。

  • Batch Normalization

    在机器学习中通常会对输入数据进行 normalization。在多层神经网络中，深层隐含层的输入取决于网络输入数据和浅层网络的参数，由于浅层网络的参数是随训练不断变化的，因此深层网络层的输入分布会随训练进行不断变化，导致训练难以收敛，对网络参数初始值的设置比较敏感。

    Batch Normalization 是在网络每层的输出与激活函数之间加入一个 BatchNorm 层，可以理解为在网络的没一层之前都作归一化的预处理，这样每层的输入都是经过归一化的。可以使每层网络的输入分布在训练时不会发生太大变化。

    具体实现

    在每层网络中，[对于每个 batch，计算该 batch 数据的在该层的均值和标准差，进行 normalization]，经过一次线性变化，再经过该层的激活函数。

    在测试时由于是一个一个数据流经网络，因此每层的均值和方差需要使用指数加权平均（Exponentially Weighted Averages） 基于训练数据进行估计。具体的，在训练的时候同时维护 minibatch 均值和方差的指数加权平均，测试时直接使用该全局均值和方差对测试数据做处理。

    Batch Normalization 的优点： 对于网络权值的初始化有更好的鲁棒性；可以使用更高的学习率；较好的防止梯度弥散；有一定的 Regularization 的效果（因为每个 minibatch 进行归一化的均值和方差都是基于该 minibatch 的数据计算出来的，带有一定的噪音，给激活层的输入引入了扰动）


Preprocessing

  • 均值减法，即每个数据都减去所有数据的均值，可以理解为讲数据迁移到原点
  • 归一化 Normalization，将数据的所有维度都归一化，使数据的范围都近似相等。一般的方法是先进行零中心化，然后每个数据除以所欲数据的标准差。
x -= np.mean(x)   # 均值为 0
x /= np.std(x)    # 标准差为 1
  • PCA 和 Whitening（白化） 另外的一种数据预处理方式，在传统机器学习中常用，在深度学习中不常用。


CNN

CNN 主要用于图像，因为图像的数据量大，直接使用全连接的神经网络会导致参数过多，训练困难。

CNN 中的主要技术:

  • 局部感知，因为图像距离相近的像素往往相关性高，无需对每个像素进行感知， 可以对局部进行感知，然后再将局部的信息集合起来。(降低参数数量)

  • 参数共享。卷积操作实际上可以看成是特征提取的一个过程，参数共享其中隐含的原理是，图像中某一部分的统计特性是和其他地方的统计特性是相似的(比如边缘提取，因此使用相同的卷积核对图像进行处理(特征提取)。一般采用多个卷积核提取图像的不同特征。

  • pooling。由于图像通常具有静态性的性质，即一个区域的特征可能在另一个区域也会出现，所以对不同的区域进行聚合统计，比如计算均值或者最大值等，可以降低特征的维度。常见的 pooling 有 max 和 average(max 效果更好)。通常是在连续的卷积后周期地插入 pooling (逐渐降低参数的数量(注意 pooling size 太大会对网络造成破坏。现在部分 CNN 倾向于使用递增的 stride 来取代 pooling。

  • 多层卷积。在 CNN 中一般采用多层卷积。因为一层卷积得到的特征往往是局部的，在之前卷积的基础上再进行卷积可以得到更加高层，更加全局化的特征。

CNN 在 NLP 领域的应用主要是用于分类(情感分析，垃圾邮件检测等)，基本结构一样，只是输入由像素矩阵变成了句子矩阵(由一个个的单词行向量叠成)
(CNN 用于处理网格拓扑结构的数据，sequence 的数据可以看作是 1 维网格的数据，因此 CNN 也可以用于处理序列的数据)

CNN 主要使用了局部连接、权值共享、pooling 等技术。本质:局部不变性和组合性
对于具有相关性的结构化数据，CNN 能够使用更少的参数(相比全连接神经网络)得到更好的训练结果 自然语言实际上经过处理 word2vec 等实际上也是一种具有相关性的结构化数据(语义相关)

  • 从局部和整体的关系。CNN 可以对数据局部的 feature 进行捕捉，由次层次的 feature 组合成高层次的 feature.一层卷积操作可以看作是由多个可学习的滤波器对圆图像进行滤波，滤波器高度和宽度通常比原图小，深度和原图一样。每个滤波器可以看作是对应一个特征(边缘等.
  • 从参数数目的角度，CNN 将全连接层与层之间的矩阵乘法变成了卷积操作，大大降低网络参数的数目，从而降低网络的训练难度(可以看成是一种 regularization)
  • 从运算的角度，CNN 在 GPU 上的实现效率非常高

CNN 基本结构:

$$ Input \to [(Conv \to ReLU)\times n \to(Pool)]\times m \to (FC\to ReLU)\times k\to FC $$

CNN 卷积后的维度变化
假设原图像输入的大小为 \((W,H)\) ，filter 大小为 \(F\) ，padding 大小为 \(P_w, P_h\)，卷积步距为 \(S\) 则卷积后输出大小为

$$ W'=\frac{W-F+2P_w}{S}+1 $$ $$ H'=\frac{H-F+2P_h}{S}+1 $$

CNN 实践中:

  • 通常 pooling 使用 max pooling
  • 通常更倾向于多个小的 filter 层叠而不是一个大的 filter
  • 通常 CNN 中卷积层参数相比 FC 要少得多，但是卷积操作会占据大量的计算和内存资源

TODO: Classic CNN architecture (LeNet, VGG, ResNet, et al.)


RNN

应用:语言模型/文本生成/机器翻译/语音识别/生成图像描述
拓展:双向 RNN / Deep RNN(多层) / gated RNN(LSTM/GRU)

  • Attention
    Attention 本质上是另一种计算 context 向量的方法，考虑到输入所有 timestep 的 hidden state，(而不是传统的只考虑最后一个 timestep 的 hidden state)。
    具体方法是对所有 timestep 的 hidden state 计算一个权重 a_t，然后加权和作为最后的 context vector。计算权重 a 的方法有几种(主要是计算每个 hidden state 的 score)，但思路都是拿每个 timestep 的 hidden state 和最后一个 hidden state 计算一个 score。计算又可以分为无参数的(直接相乘)或者有参数的(加入可训练的参数)

  • Beam search
    beam search 针对的问题是，每次 decoder 输出的时候都是选概率最高的输出，但是从输出结果整体的角度看，最优的输出的第一个并不一定是概率最高的。
    Beam search 采取的方法是在每个 timestep 输出时同时考虑 b 个可能的选项.

TODO


DL in practice

  • 确定优化目标(metric)
    • 考虑多个损失来源(比如垃圾邮件过滤中损失有将有用的标记为垃圾和没有将垃圾邮件标为垃圾(多个损失之间权重可能不同
    • 对于类别不均匀的分类问题，采用 precision 和 recall 作为 metric
  • 快速搭建一个简单的 end-to-end 模型
    • 考虑实际问题，不是什么问题一开始就考虑 dnn 模型，如果问题简单，可以先用 logistic regression 模型
    • 如果选择神经网络，考虑输入和输出的结构进行选择。(FC/ CNN / RNN)
    • Optimizer: 合理的方法一个是 momentum with a decay learning rate (线性 decay 直到一个定值，指数下降，或每次按照一个 factor decay)。另一个值得考虑的是 Adam
    • 激活函数一般考虑 ReLu 及相关变种(Leaky ReLu)
    • Regularization (early stopping / Dropout / L2 / weight decay)
  • 确定系统的瓶颈(过拟合欠拟合，原因是什么)
    • 训练数据 观察在当前训练数据下的表现，确定是否需要更多的数据。如果没有更多数据了，只能尝试对模型进行改进。如果 find tune 后还是表现很差，考察数据本身是否有问题(太多噪声
    • 如果测试集上的表现比训练集差很多，通常的解决办法就是收集更多的数据，其他的方法:减小模型大小，regulariza
    • 通常可以画出数据量和 test error 的关系，观察多少数据量是合适的
  • 改进模型，超参选择
    • 调参的目的是使模型的容量和问题的复杂度相近。(衡量标准就是 test error
    • 几个常见参数(学习率，隐层数目，卷积核大小，zero-padding，weight decay 系数，Dropout 系数)
    • 自动化探索超参
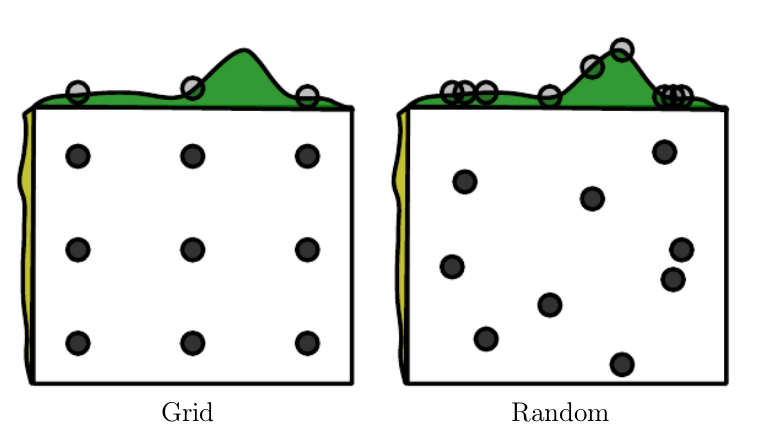
      1. Grid search
        Grid search 对于参数每个维度设定一定的取值范围，然后遍历所有组合，找到最优参数设置
      2. Random search
        不对参数进行离散化，按照模拟的概率分布 sample。效果比 Grid search 更优。
      grid_and_random_search
  • Debug 策略
    • 可视化学习效果(图像标识可以打印标识区域，语音生成可以听一下生成的语音
    • 根据 training error 和 test error 判断
    • 检查梯度(数值计算梯度(通常是自己实现梯度下降的时候可能出错了
    • 可视化 activations 和 gradients(直方图(tensorboard


模型压缩

通过对训练好的模型进行网络剪枝，剪去权值较小的连接，然后再重新进行训练（相当于通过第一次训练找到相对重要的连接，在后续的训练中只保留这些比较重要的连接。这种稀疏训练可以使得稀疏模型达到原模型的性能。

DSD 方法：

  • 密集训练，找出最要的权值连接；
  • 稀疏训练，剪去不重要的连接（由一个稀疏度参数控制），再进行训练；
  • 密集训练，将之前剪去的连接初始化为 0，重新进行密集训练，可以达到原模型更佳的性能；

这里引申另外一个问题：当前深度学习需要改进的另外一个方向，就是梯度下降方法的改进。通过压缩模型再训练可以达到与原模型差不多的性能，从侧面说明当前梯度下降的训练方法是存在局限性的。


Gradients Clipping

针对梯度爆炸的情况，可考虑使用 gradients clipping。当某一次计算的梯度太大时，会使得参数一下子冲得太远，这可以使用修剪梯度来限制梯度的大小。

gradient clipping 有两种 clip 方法：

  • 一种是超过某个阈值 \(G_{threshold}\) 直接 clip 为阈值大小

  • 一种是等比例修剪（缩放）

    $$ G'=\frac{G_{threshold}}{G_{norm}}\cdot G $$

    即保证各参数梯度比例（方向）不变，最大梯度修剪为 \(G_{threhold}\)