A Step-by-Step Neural Net Example

本文对全连接神经网络前向和反向传播进行推导，并基于 Python + Numpy 实现了一个简单的全连接网络进行多分类任务，并在Iris 数据集上进行测试。

网络结构

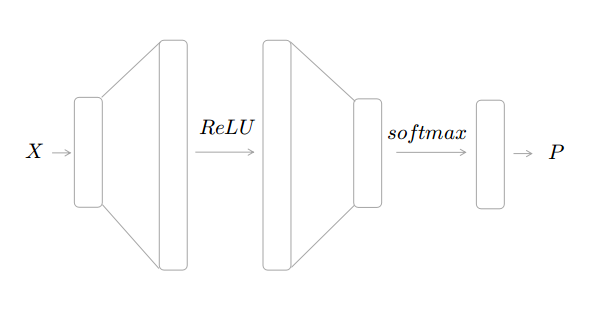
定义一个最简单的 Fully-connected neural network 进行多分类任务，只包含一层隐层，结构如下图

输入数据 X 经过一层隐层，激活函数采用 ReLU，输出层采用 Softmax 函数进行归一转化成分类概率。网络 Forward 过程计算如下：

$$ h_1=X W_1+b_1 $$ $$ a_1=\mathop{ReLU}(h_1) $$ $$ h_2=a_1 W_2 + b_2 $$ $$ P=\mathop{softmax}(h_2) $$

其中

$$ \mathop{ReLU}(x)=\max(0,x) $$ $$ \mathop{softmax}(x_i)=\frac{e^{x_i}}{\sum e^{x}} $$

python 代码

# forward
h1 = np.dot(batch_X, W1) + b1
a1 = relu(h1)
h2 = np.dot(a1, W2) + b2
p = softmax(h2)

参数初始化

神经网络的参数初始化在很多时候对模型训练影响非常大，不恰当的初始化方式会导致学习缓慢甚至失败（比如全零初始化）。关于参数的初始化方法有很多更深入的研究，可以参考 CS231 weight_initialization。这里采用常用的Xavier 方法初始化，即参数 W 从下面的均匀分布中采样得到：

$$ W\sim U(-\frac{\sqrt{6}}{\sqrt{n_{in}+n_{out}}},\frac{\sqrt{6}}{\sqrt{n_{in}+n_{out}}}) $$

其中 $n_{in}, n_{out}$对应输入和输出的个数。

由于参数 W 的初始化已经打破了网络的对称性，因此参数 b 的直接初始化为 0 即可。

python 代码

# weight initialization
bound1 = np.sqrt(6.0 / (in_dim + hidden_dim))
W1 = np.random.uniform(-bound1, bound1, size=[in_dim, hidden_dim])
b1 = np.zeros(20)
bound2 = np.sqrt(6.0 / (hidden_dim + out_dim))
W2 = np.random.uniform(-bound2, bound2, size=[hidden_dim, out_dim])
b2 = np.zeros(3)

损失函数

多分类问题的损失函数一般采用负对数似然损失(Nagetive Log-Likelihood Loss)，即

$$ L_{NLL}=-\sum_{i}y_i \log p_i $$

其中 $p_i$ 是网络对第 i 类的输出（即预测概率）， $y_i$ 为第 i 类对应的 label。

反向传播

梯度下降的算法的基本思想就是（在定义好损失函数之后）计算损失关于各参数的梯度，使用这个梯度进行参数更新。因此我们的目标就是计算 $\frac{\partial L}{\partial W_1}, \frac{\partial L}{\partial W_2}, \frac{\partial L}{\partial b_1}, \frac{\partial L}{\partial b_2}$。只需要对应网络 forward 的过程，根据链式法则即可以计算所要的梯度。以求解$\frac{\partial L}{\partial W_2}$为例子，根据链式法则有：

$$ \frac{\partial L}{\partial W_2}=\frac{\partial L}{\partial P}\cdot\frac{\partial P}{\partial h_2}\cdot\frac{\partial h_2}{\partial W_2} $$

逐项看，第一项 $\frac{\partial L}{\partial P}$ 是损失函数关于网络输出的偏导，他们之间的关系是 $L=-\sum_{i}y_i \log p_i$，求导得到

$$ \frac{\partial L}{\partial P}=-\frac{y_i}{p_i} $$

第二项 $\frac{\partial P}{\partial h_2}$ 概率 p 关于 h2 的偏导，他们之间的关系是

$$ p_i=\mathop{softmax}(h_{2i})=\frac{e^{h_{2i}}}{\sum e^{h_2}} $$

假设输出是 k 维，则 $P$ 和 $h_2$ 都是 k 维向量，我们需要求 $\frac{\partial p_i}{\partial h_{2j}}$，其中 $i, j \in 1,...,k$。

这里分两种情况讨论，对于 $i=j$：

$$ \begin{align} \frac{\partial p_i}{\partial h_{2i}}&=\frac{\partial }{\partial h_{2i}}(\frac{e^{h_{2i}}}{\sum e^{h_2}}) \\ &=\frac{e^h_{2i} (\sum e^{h_2}-e^{h_{2i}})}{\sum e^{h_2}\cdot\sum e^{h_2}}\\ &=p_i(1-p_i) \end{align} $$

对于 $i\neq j$：

$$ \begin{align} \frac{\partial p_i}{\partial h_{2j}}&=\frac{\partial }{\partial h_{2j}}(\frac{e^{h_{2i}}}{\sum e^{h_{2j}}})\\ &=\frac{-e^{h_{2i}} e^{h_{2j}}}{\sum e^{h_2}\cdot\sum e^{h_2}}\\ &=-p_i p_j \end{align} $$

把这两种情况代回 $\frac{\partial L}{\partial P}$，得到

$$ \begin{align} \frac{\partial L}{\partial h_2}&=\frac{\partial L}{\partial P}\cdot\frac{\partial P}{\partial h_2}\\ &=-[y_i(1-p_i)-\sum_{i\neq j}y_i p_j] \\ &=p_i-y_i \end{align} $$

可以看到 $\frac{\partial L}{\partial h_2}$求出来的结果非常简洁（这也是使用 softmax 做归一化的一个原因），只需要拿网络输出向量 p 减去真实标签向量 y，得到的就是 $h_2$ 关于 $L$ 的梯度。

回到上面的式子的第三项 $\frac{\partial h_2}{\partial W_2}$，这项比较简单，求导结果为 $a_1$ 。

综合以上结果，我们就得到损失 $L$ 关于参数 $W_2$ 的梯度

$$ \begin{align} \frac{\partial L}{\partial W_2}&=\frac{\partial L}{\partial P}\cdot\frac{\partial P}{\partial h_2}\cdot\frac{\partial h_2}{\partial W_2} \\ &={a_1}^T (P-Y) \end{align} $$

其中 P 为网络输出向量，Y 为真实标签向量。关于这里矩阵相乘的顺序以及转置，只需要根据矩阵的维度进行调整，保证最后梯度的维度应该是和参数的维度是一致的即可。

对于其他参数 $b2, W1, b1$的计算也是同理，最后得到

$$ \frac{\partial L}{\partial b_2}=\frac{\partial L}{\partial h_2}=P-Y $$ $$ \frac{\partial L}{\partial W_1}=X^T (P-Y) {W_2}^T $$ $$ \frac{\partial L}{\partial b_1}=(P-Y) {W_2}^T $$

反向传播代码如下：

# backward
dl_dh2 = p - labels
dl_dW2 = np.dot(a1.T, dl_dh2)
dl_db2 = np.sum(dl_dh2, 0)
dl_da1 = np.dot(dl_dh2, W2.T)
da1_dh1 = (h1 > 0).astype(float)  # Derivatives of ReLU
dl_dh1 = dl_da1 * da1_dh1
dl_dW1 = np.dot(batch_X.T, dl_dh1)
dl_db1 = np.sum(dl_dh1, 0)

训练及结果

在得到各个参数梯度后即可对参数进行更新了，这里使用原生的 mini-batch Gradient Descent，即次拿一个 batch 数据计算这个 batch 的梯度进行参数更新。现在的神经网络训练方法一般使用改进的梯度下降，包括引入 Momentum，包括自适应学习速率的方法，感兴趣的可以参考这篇 post Optimization Methods of Deep Learning。

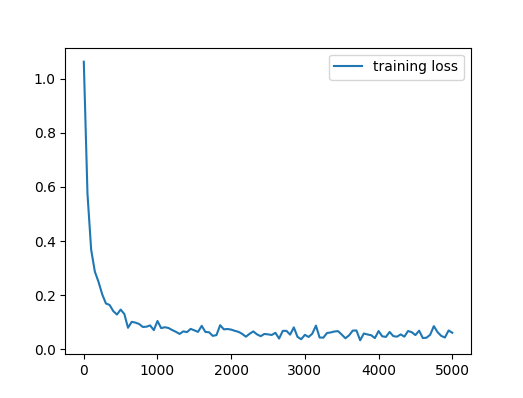
模型其他超参数设置为 batch_size 为 8，learning_rate 为 0.003，训练步数 1000 步，最后在测试集上的 accuracy 为 96%。下图是训练过程的 loss。

关于这篇 post 的详细代码见 raw_nn。可以看到这个 task 非常简单，在没有对超参进行任何调优情况下，就已经有 96%的准确率了。

总结

现在主流的深度学习框架基本上都带有更加方便的可以自动求导，写个分类也就几行代码的事，实际应用中直接使用这些工具即可。这里主要是梳理一下反向传播的过程，自己动手实现一下，防止框架用久了手生。

Guibo Wang