Reinforcement Learning Notes


Abstract

学习强化学习(Reinforcement Learning)过程中的总结，以及阅读 RLAI 的一些零碎读书笔记。


Intro

强化学习属于机器学习(Machine Learning)下的一个子领域。经典的机器学习包括监督学习(supervised learning)、无监督学习(Unsupervised Learning)和强化学习。监督学习主要是利用带标注的训练数据，调整模型参数，使在未知数据上达到性能要求的一类算法，主要包括分类和回归两大类，其主要关注的核心是在已知数据上训练一个对于未知数据具有优良泛化能力的模型。无监督学习则是对未标注的数据进行计算，挖掘数据内部的结构和模式，主要有聚类算法，其关注的核心是在如何发掘内在联系以及如何衡量挖掘的性能。

强化学习则一种 Agent 与环境 Environment 交互的模型，具体来讲，在每个时刻，Agent 从环境接收状态 state，根据状态以及当前策略 policy 作出决策 action，环境转移到下一个状态 state2，并返回一个奖赏信号 reward，Agent 根据 state2 和 reward 更新策略，继续作出动作，如此循环进行。RL 算法的目标就是找到一个最优 policy，最大化 Agent 未来 return(累计的 discounted reward)的期望值。 我们常用一个马尔科夫决策过程(Markov Decision Process)来描述这个过程，一个 MDP 可以定义为一个 4 元组{S，A，P，R}，其中 S 为环境的状态空间，A 为 Agent 的动作空间，P 为环境的状态转移概率，R 为环境的奖赏函数。



Reinforcement Learning 和 Supervised learning 的区别

模型的输出与监督信号

  • 监督学习的输出(以分类为例)是一个分类结果，其监督信号来源于训练数据中正确的分类结果
  • 强化学习的输出是动作，其监督信号来源于环境的 reward 信号

监督信号的强弱

  • 监督学习的监督信号更强，告诉模型正确的输出应该是怎样的，进而调整模型参数
  • 强化学习是通过环境反馈的 reward 信号进行学习，目标是最大化未来 reward 的期望，(不告诉正确的做法，而是允许模型去探索

一个直观的例子：比如要训练小狗听到 sit 即坐下，你并不会告诉他听到 sit 就应该两只前爪收起来，身子立起来呈坐姿，相反你会在他某次正确的 sit 之后给他食物(reward)，经过一定次数的训练后狗就知道怎么做就能得到食物。前者告诉每一步正确做法是监督学习，后者对他每一步作出反馈让他自己学则是强化学习。



Dynamic Prigramming

Policy iteration(PI)和 Value Iteration(VI)是动态规划(DP)下通过迭代寻找最优策略(control problem)的两种不同方法。两种方法都可以分为两步进行：Policy Evaluation 和 Policy Improvement。 PI 从字面上理解就是对 policy 进行迭代更新。PI 在 Evaluation 这一步是对当前策略 iterative evaluate 直至各状态 value 值收敛，即更新 value function 使其与当前 policy 相符合；然后第二步 Improvement，根据 value function 基于贪婪策略更新 policy。两步迭代交替，最终收敛得到最优 policy 和最优 value function。而 VI 相比 PI，在第一步 Evaluation 时无需 evaluate 至收敛(即只对所有状态 sweep 一次，得到 value function 不与任何 policy 相对应)，第二步 Improvement 与 PI 相同。可以证明这样也可以最终收敛，通常情况下采用 VI。

在强化学习中，DP 主要用于 model-base 的环境，在某个状态 s 下根据当前策略采取某个动作 a，所得到的下一状态 s’的概率分布是确定的(即环境模型是确定的，比如最简单的方格世界，在坐标(0,0)的状态下采取向右走的动作会转移到坐标为(0,1)的状态)。在这样的环境下怎么进行 prediction 呢，即怎样进行 policy evaluation 呢？因为环境模型是确定的，所以我们可以按照当前的 policy π 选择一个动作 a，得到 reward r 和下一状态的概率 s’分布，然后利用公式进行更新。一个问题是当前 t 时刻的 value function V(s)的计算涉及到了下一时刻(t+1)的 value function V(s’)。在实际计算中我们采用当前时刻 t 对下一状态 s’的估计来代替原式中下一时刻 t+1 对下一状态 s’的估计，也就是当前状态 value function 的估计，是基于当前对下一状态的估计(当然还有执行动作后获取的 reward)的，具有这种性质称为 bootstrap(自举).

之所以说 DP 用于 model-base 环境是因为 DP 算法在计算某个状态 s 的 value function 的时候，考虑了在当前的 policy 下可能产生的所有动作以及所有后继状态，这就要求 agent 要有环境的先验知识才能进行计算。这在很多现实问题中都是很难实现的(比如二十一点，你不可能知道在当前状态下执行某个动作(补牌、保持)以后后继状态(炸、赢庄家、输庄家)的概率分布。下文要说的 model-free 的方法则不要求 agent 具备环境的先验知识就可以进行 evaluate.

DP 的思想很重要，后面的 MC 和 TD 都是在非严格的 MDP 中实现类似动态规划的思想。其核心思想是使用 value function 来组织策略的搜索和优化，只要找到最优的值函数，就可以得到最优策略。

DP 的求解分两步循环迭代：

  • Policy evaluation (对于任意策略计算值函数
  • Policy Improvement (基于估值函数，进行策略的优化

根据 evaluation 这一步的不同，又可以分成 policy iteration 和 value iteration 两种方法。Policy Iteration 是每次 evaluation 都估计直至值函数收敛

eval(till converge) -> improve -> eval(till converge) -> improve -> …..。

而 Value Iteration 是在 evaluation 这一步只 evaluate 一次，而不是 evaluate 直到收敛。这样加快训练速度并且依然保证最后 policy 的收敛。

eval(one sweep) -> improve -> eval(one sweep) -> improve -> ……



Monte-Carlo(MC) Methods

前面讲到，在具备环境 model 的情况下，可以使用 DP 直接对状态进行估值，进而根据贪婪策略选择让下一状态价值(V 值)最大的动作。而现实问题中大部分 model 都是不可知的（也就是你不知道采取这个动作会转移到什么状态），在没有 model 的情况下对状态进行估值后，并不知道采取哪个动作会转移到 value function 最大的下一状态(执行动作后的无法得到下一状态的概率分布)。因此考虑直接对 state-action 估值(Q 值)，估计在状态 s 下采取动作 a 的价值 Q(s,a)，这样只需简单选择 value-action 最高的动作执行，不必考虑环境的概率分布。

MC 通过不断地在环境中 sample，得到一系列 episode。在每个 episode 中，可以计算得到该 epidode 中所出现的各个状态的估计回报值，对于每个状态，将多次 episode 得到的多次估计回报的平均作为该状态的价值估计。因此，MC 策略的更新是 episode by episode，即走完一个 episode，更新这个 episode 里面出现过的所有状态的 Q(s,a)。当所有状态访问过足够多时，其 Q 值会逐渐收敛于真实 Q 值。

因此 MC 不依赖环境模型(状态转移概率)，只需不断地从环境中 sample experiences，只用 return 均值去更新 Q 值，直至 Q 值收敛，达到最优策略。这也是 MC 方法名称的来源。(Monte-Carlo 的思想就是从大量的样本中去估计)



Temporal Difference(TD) Learning

TD 是 DP 和 MC 的结合。强化学习中最核心的方法。

  • 和 MC 类似，TD 直接从 experience 中学习(不要求知道环境的状态转移)
  • 和 DP 类似，TD 基于当前的估值函数对估值函数进行更新(bootstrap)，而不用等到 episode 结束再进行更新。

最常使用的 TD 方法包括 Q-learning(off-policy)和 SARSA(on-policy)。



Function Approximation

使用传统表格得到 value function 受限于状态、动作空间，不适用于解决实际问题。Lookup table 是维护一个状态 s(或者状态动作对 s-a)然后每次到表里去查找对应的 v(s)或者 Q(s，a)，本质上就是一种特殊的 mapping，因此可以 generalize 到更一般的情况，使用某种函数进行拟合（function approximation）。 输入状态 s 或者状态动作对 s,a，经过拟合函数的映射，得到 V(s)或 Q(s,a)，那么就能解决 lookup table 的局限性，实现泛化。（即有些状态即使没有见过，但是同样可以求出 V 和 Q）

Function approximator 有很多种，包括神经网络、线性特征组合(线性回归)、决策树、kNN 等。在 RL 中考虑可微的 approximator，因为我们是知道优化目标的(使用 MC 或者 TD 等求得)，所以可以通过梯度下降来使函数不断逼近我们想要的 mapping。

假设以线性回归作为 approximator，假设模型参数为 \(W\)，模型输入 \(X\) 由表征状态 s 的某些 feature 组成，则模型输出为值函数估值 \(h=W^T X\)，已知 target 值 \(y\) (MC 或者 TD 得到)，则可以将误差表示为

$$ L=\frac{1}{2}(y-h)^2 $$

接着利用梯度下降对特征的参数求偏导，并基于求得的梯度对参数进行更姓。

$$ \frac{\partial L}{\partial W}=(y-h)X $$ $$ W=W-\alpha \frac{\partial L}{\partial W} $$

其中α为梯度下降的学习率。

这样这个线性回归模型就是一个值函数的函数拟合器，他反映了一种状态 s 和 value function 的映射关系。

NOTE

  • 其实 Lookup table 本质上是线性回归的一种特殊情况，其对应 X 是一个 0-1 向量，当前状态的特征是值为 1，其他状态的特征都是 0。
  • 在使用非线性函数（比如神经网络)作为函数拟合器时是没有收敛保证的(由于数据间的强相关性和不稳定性)。使用神经网络作为强化学习中估值函数的拟合器最早的应用是 TD Gannon， 而 DQN 的成功使得基于神经网络的强化学习在近几年又重新受到关注。（DQN 中采用了两个主要的方法克服收敛问题，一个是 experience replay，一个是 target network）。



On-policy vs Off-policy

  • On-policy：学习的策略与当前决策的策略是一致的。通过 policy 选择动作，进而学习优化该 policy。
  • Off-policy：学习的策略与当前决策的策略可以不一样。使用 policy_act 来选择动作，进而训练 policy_target。

以 Q-learning 和 SARSA 作为例子。在 Q-learning 的中，当前决策的策略是选择 Q 值最大的动作，而学习的策略是通过计算 TD-error：

$$ \mathop{Error}_{t}=\mathop{TargetQ}_t - Q(s_t，a_t) $$ $$ \mathop{TargetQ}_t= r(s_t,a_t)+\lambda \max_a Q(s_{t+1}，a)$$

其中 Target Q 是选择下个状态 \(s_{t+1}\) 中 Q 值最大的动作计算得到，这是“另外”的一种 policy（区别于当前决策的策略）。因此(tabular)Q-learning 属于 Off-policy 的方法。

SARSA 的决策的策略也是选择 Q 值最大的动作，但是 SARSA 学习时的 TD-erro 是

$$ \mathop{Error}_{t}=\mathop{TargetQ}_t - Q(s_t，a_t) $$ $$ \mathop{TargetQ}_t= r(s_t,a_t)+\lambda Q(s_{t+1}，a_{t+1})$$

其 Target Q 是基于当前的策略计算出来的(\(Q(s_{t+1}，a_{t+1})\))，即使基于当前策略 -> 得到 TD error -> 更新当前策略，故属于 On-policy。

NOTE:

虽然 DQN 是基于 off-policy 的 Q-learning 的算法，但由于使用神经网络对估值函数进行拟合，使得更新公式中 Target Q 的计算还是依赖于当前网络的参数(当前的 policy)，因此其实并不是真正完全地 off-policy。这样可能导致的一个问题是，当神经网络更新 s 状态下 Q(s，a)时，临近状态 s’的估值 Q(s’，a)也很可能发生改变(神经网络的更新是更新网络参数)，即 targetQ y 也发生改变，容易造成学习过程难以收敛。

这就是 DQN 中引入 Target Network 的一个重要原因，通过采用一个额外的 Target Network 专门用来计算 TargetQ，每隔一定 episode 就将当前 Q Network 参数复制到 Target Network，然后在接下来的一定 episode 中 Target Network 保持不变，使 DQN 变成完全的 off-policy 算法(学习的策略和决策的策略不相关)，可以提高训练的稳定性。



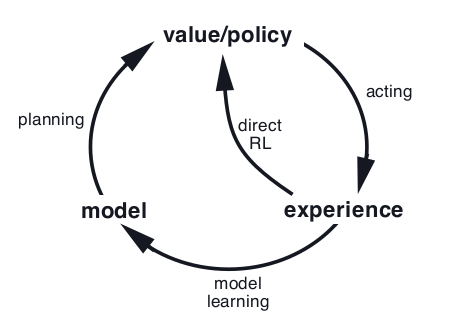
Model-free & Model-based

RL 算法的一种分类方法是分成 Model-free 和 Model-based 两种.

两者最核心的区别就是 agent 在与环境交互的过程中有没有尝试去“了解”环境(i.e.环境的状态转移概率、奖赏函数等)。若没有，只是单纯地接收环境的状态、奖赏，根据这些 experience 进行更新，成为 model-free 算法，目前大部分 RL 算法属于 Model-free 算法，一个原因是在大多数问题中，环境模型和奖赏函数过于复杂，很难学习到。Model-free 算法往下又可细分为 Value-based 和 Policy-based，另说。假若 agent 在交互过程中同时学习环境模型(在“脑海”中构建环境的模型)，则成为 Model-based 算法。

  • Model-free Model-free RL 可以分为 Value-based 和 Policy-Based 两大类。Value-based 包括 Monte Carlo 和 TD(Temporal difference)。Polic-based 主要是基于 Policy gradient 理论的算法和其相关的变种。此外也存在 value-based 和 policy-based 结合起来的算法 Actor-Critic，即使用值函数辅助进行 policy gradient 的计算。

  • Model-based Model-based 算法通过 experience 学习一个环境的 model(状态转移 P，奖赏函数 R)，model 本质上是环境 MDP 的一个 representation(P，R)，可以使用监督学习从 real experience 中学习得到。 得到这个自己构建的(也许不那么准确的)model 之后，可以进行 sample，产生 simulated experience。 这样就同时拥有了真实世界产生的 real experience 和 agent“想象”出来的 simulated experience，有两种做法：

    • 单独使用 simulated experience 学习 value function / policy,
    • simulated experience 和 real experience 结合起来同时进行学习(Dyna)，其中通过 real experience 学习为 direct RL
model_based_rl

Planning as part of action selection

得到 model 后，可以利用这个模型来进行 planning(规划)，作出更好的决策。 具体方法是：在某个 state 要作出动作前，都进行 planning。从当前 state 向前规划(使用 model)，再使用 model-free 的 RL 方法学习。即每一步 planning 学到几个 Q 值，选择最佳的动作实际执行，进入下个状态，抛弃之前的 planning，重新进行新一轮的 plannig(当状态空间很大，状态重复出现的概率不高，没有必要保存)。

MCTS

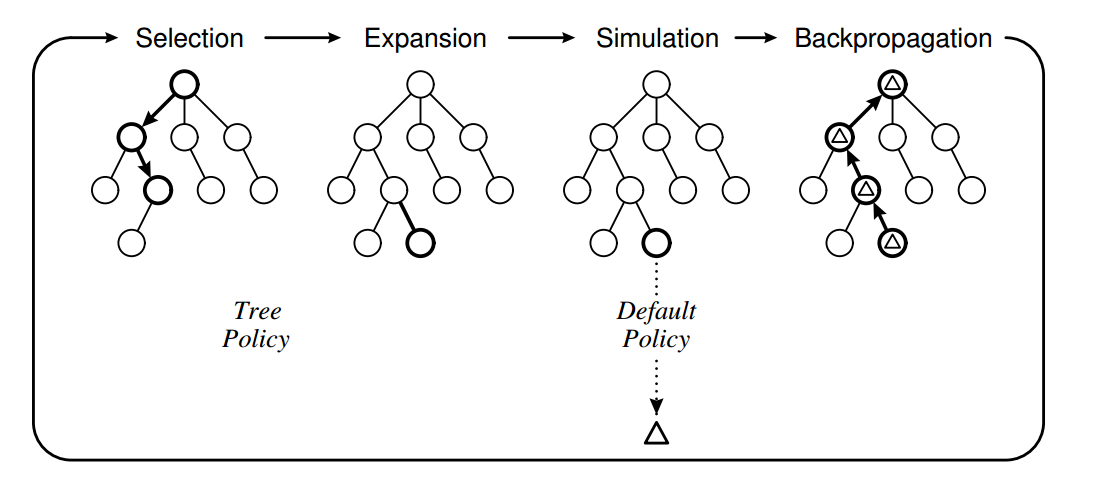
MCTS 是 planning as part of action selection 的一种方法，在当前状态下 agent 使用一个简单的 simulate policy 产生很多的 trajectory，在”脑中”进行 planning，然后作出决策。 MCTS 在某个状态下基于 model 和一个 simulate policy 逐渐地构建一课(partial) game tree，树中的节点表示状态，连接节点的边表示连接两个状态的状态动作对 节点中维护两个值(经过这个状态赢的次数，经过这个状态的 trajectory 总数)，只要 trajectory 足够多，这两个数的比值就趋近与该 state 的真实值。

基本 MCTS 的流程:

  1. selection

根节点为当前 state，当所有可能 next state 都已经在树中时 [1]，根据 Tree policy [2] 选择一个策略继续往下走，直至某个 state 有未访问过的 next state(没有在树中)，此时进行下一步 expansion

  1. expansion

当某个 state 存在没访问过的 next state 时，此时从未访问过的 next state 中随机 [3] 选择一个 next state

  1. simulation

接着从 expand 的这个节点开始往下按照 default policy [4] 进行仿真(在脑海中模拟后续发展

  1. back-propagation

某次仿真结束 [5] 后得到最后的分数，沿路返回更新沿途的节点的值.

以上 4 步在根节点这个状态下选择动作时迭代进行，直至最后超出一定的限制(树的规模或者计算时间)结束，然后统计根节点下哪个节点最好，最后在真实世界中执行一步动作。

mcts

[1] 不一定要所有 next_state 都已经在树中才进行 select(对于状态空间很大的 task 比如围棋其搜索树的宽度会异常大)，在某些 task 中不必探索所有的 next state。如果知道了具体某个 task 的先验知识时，我们可以对树的宽度进行剪枝。在 AlphGo 中便使用了 policy_human(模拟人类走棋的网络)对宽度进行剪枝，即只考虑人类比较有可能的走子往下探索(先验知识 [2] Tree policy 可以使用随机，也可以使用 UCB 算法，使用 UCB 算法的 MCTS 成为 UCT [3] 当要进行 expand，选择未访问的节点时，可以用随机，同样也可以通过嵌入先验知识选择比较好的节点进行 expand [4] default policy 可以简单地使用随机，也可以使用其他 policy(这个 policy 就是在脑海中模拟走子的 policy) [5] 不一定要仿真到最后出结果(状态空间很大的 task 每次 simulate 都会花费很长时间)，可以借用值函数，仿真到一半就暂停，使用值函数对当前仿真到的状态进行估值，然后回溯。相当于在深度方向上进行剪枝。

MCTS 目前比较成功的应用还是在游戏特别是棋盘游戏方面，AlphaGo 就是 MCTS 应用最成功的例子。因为棋盘游戏的模型是已知的，采取某个动作转移到某个状态是确定的，因此可以采用这个 model-based 方法进行 planning。当然 AlphaGo 中对 MCTS 进行了一些改进(剪枝)，但是本质上还是 MCTS 的思路.

MCTS 参考资料： MCTS survey A simple MCTS demo on game of Tic-Tac-Toe



AlphaGo

AlphaGo 是由多个组件拼装起来的一套系统，主要组成部分有一个模仿人类走棋的 policy network，一个通过强化学习自我博弈得到的网络 policy_plus network，一个值函数网络 value network。最后通过 MCTS 框架把三者融合起来。

基本思路如下：

  1. 首先简单训练一个模仿人类走棋的网络(分类任务，数据是人类棋谱)，不考虑局势输赢，简单暴力模仿 P_human
  2. 使用增强学习自我博弈，使用 P_human ，考虑输赢 reward，REINFORCE 算法，得到 P_human_plus P_human 和 P_human_plus 的区别是，P_human 更发散，考虑更多可能的情况， P_human_plus 相对更集中于他认为较优的选择
  3. 使用 MCST 进行搜索，当然不是随机搜索，而是基于 P_human 的选择进行搜索，即在人类比较可能走的位置中进行深入搜索
  4. 引入估值函数 v()，估值函数的训练如下：
    • 首先使用 P_human 走 L 步，L 为随机步数，(模拟不同阶段可能出现的局面)记录此时的状态 s
    • 之后使用 P_human_plus 进行互搏，并记录最后的结果 r
    • 通过训练<s，r>得到估值函数，表示表示在某个状态下双方都使用 P_human_plus 策略时我方赢的可能性

NOTE：这里训练时如果全部使用 P_human 效果不如使用 P_huamn_plus

  1. 将估值函数融合进 MCTS 框架中

估值函数的作用是用在蒙特卡洛搜索时的分数估计，原本没有使用估值函数时分数估计公式如下

新分数=调整后的初始分+通过模拟得到的赢棋概率

融入估值函数后分数估计公式如下：

新分数=调整后的初始分+0.5×通过模拟得到的赢棋概率+0.5×局面评估分

因此本质还是 MCST，只是使用了 P_human_plus 对搜索树进行宽度修剪，使用估值函数对树深度进行修剪，使其能够应对围棋巨大的状态空间。



Deep RL Tunning Skills

Both Deep Learning and Reinforcement Learning algorithms are hard to optimize。Here are some optimizing/tunning skills of Deep Reinforcement Learning。

For a new algorithm

  • use a small test problem and build the system quickly
  • do hyperparameters search (grid/random search)

For a new task

  • provide good input features
  • shape reward functions
  • see if observations and reward are on a reasonable scale

Training stuff

  • use multiple random seeds
  • using running average to standardize if observations have unknown range
  • rescale rewards but don’t shift mean
  • standardize prediction target
  • print min/max/stdev/mean of episode return，episode length

For policy gradient methods

  • observe policy entropy
  • policy initialize: zero or tiny final layer

For Q-learning

  • optimize memory usage (when using replay buffer)
  • learning rate schedules

更多 DRL tunning skills 参考: The Nuts and Bolts of Deep RL Research



RL is hard

RL 难优化的一个关键就在与动作存在 延迟反馈 的性质。即虽然环境反馈的 reward 是监督信号，但是这个监督信号与当前的动作不一定具备直接对应的关系，即无法单纯通过当前时刻的反馈来判断当前状态下采取当前动作的好坏。

为了解决这个问题，我们可以对状态和动作进行估值。通过估计某个状态或者某个状态下采取某个动作的价值，即 V(s)和 Q(s，a)，进而根据估值作出决策。V(s)表示在 s 状态下的未来累计回报的期望值。Q(s，a)表示在状态 s 下采取动作 a 的未来累计回报的期望值。只要求得状态空间和动作空间中所有的 V(s)或 Q(s,a)，就可以得到我们的策略——每次选取最大的 V(s)或 Q(s,a)进行状态转移。(回想下 RL 的目标就是最大化未来累计回报期望值)。因此我们只要正确地估值就能保证最后的策略是最优的。这种基于估值函数间接得到策略的思想是 RL 中最重要的思想之一，在此思想基础上发展出来的 Value-based 的方法也是应用最广泛的 RL 算法。

相比 Value-based 曲线救国的思路，policy gradient 方法则直接地多，直接通过计算(估计)当前策略的梯度，使策略往好的方向改进. 以下棋作为一个便于理解的例子。在一盘棋中每一步棋作为一个动作，一直走到最后赢或者输才会得到一个 reward，其他时候 reward 都是 0。policy graient 的思路就是如果最后结果赢了(reward 为正)，那么就把这一局所有的 action 都视为好的 action，提高对应状态下采取对应动作的概率；反之则降低。这样的方法直觉是有失公允的，就是上文提到的 RL 的关键问题，某一步好棋并不一定使最后能赢，输局中并不是所有的棋步都是坏棋。即我们把所有的动作的好坏都“混合”到一起，混为一谈了(导致这个更新的 variance 非常高)。理论上这样的方法是行得通的，但是需要非常非常多的局数才能够逐渐学习到正确的策略。

作为对比，Value-based 的方法则是每走一步就就当前的动作的价值进行更新(基于当前的估计，即 bootsrap)，从而避免了一局里面的所有动作一视同仁，从而降低了 variance。但是由于是基于估值进行更新的，估值会由偏差，即使用 value-based 的方法会有 bias。



Policy Gradient Methods

前面 DP、MC、TD 等方法的核心都是基于估值函数，即学习状态 s（或状态动作对 s-a）的价值，进而得到最优策略，统称为 value-based 的方法。而 Policy Gradient 则是区别于 value-based，不借助估值函数，而是直接使用函数拟合器（神经网络等）表示策略，求解策略的梯度，对策略进行优化，最终得到最优策略，属于 policy-based 的方法。policy gradient 在我们看来是更加直接的方法，实际上 policy-based 的方法的提出时间也要早于 value-based 的方法，但是由于相比 value-based 的方法收敛较慢等缺点，使后来的发展没有 value-based 方法快。但是当人们发现了神经网络与强化学习结合的威力后，回过头再看 policy-based 方法，实际上对于很多现实中的困难问题，使用 policy-based 方法比使用 value-based 方法更佳。