ML Q&A


本文整理 Machine Leanring 一些相关问题。


目录

线性模型

线性回归为什么使用均方差作为损失函数？

使用均方差损失函数，实质上是最小二乘法的思想，使用平方来度量观测距离，最优拟合直线使各点到直线的距离之和（平方和）最小。 在误差\(\varepsilon\)服从高斯分布的前提下，使用极大似然估计法可以得到最小二乘式子，其形式与均方差相同。

假设误差服从高斯分布：

$$f(\varepsilon_i;u,\sigma^2)=\frac{1}{\sigma\sqrt{2\pi}}\exp(-\frac{(\varepsilon_i-u^2)}{2\sigma^2})$$

似然函数：

$$L(u,\sigma^2)=\prod_{i=1}{N}\frac{1}{\sigma\sqrt{2\pi}}\exp(-\frac{(\varepsilon_i-u^2)}{2\sigma^2})$$

对数似然：

$$\log{L(u,\sigma^2)}=-\frac{n}{2}\log{\sigma^2}-\frac{n}{2}\log{2\pi}-\frac{\sum_{i=1}^{N}(\varepsilon_i-u)^2}{2\sigma^2}$$

求偏导,最大化对数似然：

$$u=\frac{1}{N}\sum_{i=1}^{N}\varepsilon_i$$ $$\sigma^2=\frac{1}{N}\sum_{i=1}^{N}(\varepsilon_i-u)^2\approx \frac{1}{N}\sum_{i=1}^{N}(y-y_i)^2$$

可以看到求极大似然估计法令\(u,\sigma^2\)偏导为 0，最终的形式与最小化均方差的形式是相同的。


线性回归、Ringe、LASSO 的关系？

在误差服从高斯分布的前提下，均方差损失函数->最小二乘->极大似然估计（最大后验概率）
更进一步，在误差服从高斯分布的前提下：

  • 如果参数\(w\)服从高斯分布，则通过最大后验推导出来最后即为 Ringe 回归（加上 L2 正则项的线性回归）
  • 如果参数\(w\)服从拉普拉斯分布，则最后推导出来即 LASSO（加上 L1 正则项的线性回归）

详细推导参考：这里


Linear SVM 和 Logistic Regression 的比较？

相同：

  • 都是线性分类器，本质上都是求解一个超平面。很多情况下两者的性能接近。
  • 分别采用 logistic loss 和 hinge loss，本质上都是增加对分类结果影响较大的样本的权重，减小对分类影响较小的样本的权重。

不同：

  • LR 改变权重的方式是通过 sigmoid 映射，减小离分类平面较远的数据的权重，增加离分类平面较近的数据权重；而 SVM 则是直接考虑 support vector，即与分类最相关的数据点取学习分类器。
  • SVM 最后的分类超平面是有几个支持向量决定的，对于一个训练好的 SVM 分类模型，增加或删除支持向量 gap 之间的数据点对分类结果是没有影响的；而对于 LR，每个数据点对最后的模型都是有影响的 （具体的影响随数据点到平面距离的增加而递减）
  • Linear SVM 和 LR 在低维小数据量上表现差不多，但是在高维数据上 LR 表现更好。（因为 Linear SVM 依赖于数据表达的距离测量，在高维下这个刻度可能不好，一般需要做 normalization）
  • SVM 转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时速度更快；

NOTE：

  1. 感知机模型也是划分一个超平面，不同的是感知机是通过最小化误分类点到超平面的距离之和，而 LR 是将分离超平面作为 sigmoid 的输入，输出正负样本的概率，通过极大似然估计最大化后验概率分布，SVM 则是通过最大化样本到超平面的最小距离确定超平面
  2. 两者都可以通过 kernel trick 解决数据非线性可分的问题


集成方法

Boosting 和 Bagging 比较？

  • Bagging 的弱学习器之间不存在依赖关系（易并行），Boosting 的弱学习器之间存在依赖关系（较难并行）

  • Bagging 偏向于减少方差 variance，Boosting 偏向于减少偏差 Bias。对于 Bagging 而言，我们希望单个弱学习器关注减少 Bais（因此采用比较深的决策树），但是弱学习器之间差异性比较大（随机属性选择），通过集成以降低模型的 variance；对于 Boosting，每次个弱学习器都会在上一轮的基础上进行拟合，可以保证模型的 Bias，因此对于单个弱学习器而言，我们选择比较简单的分类器（深度很浅的决策树）以保证 variance 比较小。

  • Intuitively, Bagging 是每个人都专精一个领域，不同的人攻克不同的领域，最后组合起来。Boosting 是每个人可以不那么精通，但是每个人的领域要尽量一致，一起做一件事情。


Bagging 中为什么常使用决策树作为 weak learner？

  • 通常希望 基学习器具有低偏差、高方差的性质（overfitting 趋势），经过 Bagging 后能够在增加一点偏差的同时大大减少方差。
  • 未剪枝的决策树具有这种性质，线性学习器一般属于较稳定的学习器（不容易 overfitting）
  • 数据样本的扰动对决策树的影响较大，因此不同子样本集训练的决策树随机性较大（不稳定学习器）


Random Forest 和 GBDT 的比较？

相同：

  • 两者都是使用决策树作为基本的弱学习器

不同：

  • RF 是 bagging 的思想，弱学习器之间不存在依赖关系；GBDT 是 boosting 的思想，当前的学习器依赖于之前的学习器


GBDT 和 XGBoost 的比较？

  • 前者更多是指一种机器学习算法，后者是该算法的工程实现
  • GBDT 以 CART 作为弱分类器，XGBoost 不仅可以使用树作为弱分类器，还支持线性分类器
  • GBDT 在优化时候只使用了一阶导数信息，XGBoost 在优化时进行了二阶泰勒展开， 同时使用了一阶和二阶导数信息
  • XGBoost 支持自定义损失函数（只要损失函数一阶二阶可导）
  • XGBoost 在损失函数中显式地加入了正则项（叶子节点的个数、每个叶子节点输出的 score 的 L2 模平方），控制模型复杂度，防止过拟合。本质上相当于对树进行剪枝，但与 GBDT 构建完决策树再回头剪枝不同，XGBoost 在分裂的过程中就考虑的正则化
  • XGBoost 借鉴了随机森林，构建每棵树的时候支持列抽样（columns subsampling）
  • XGBoost 进行了并行优化。这个并行不是在树粒度上的并行，树还是串行生成的，并行是在特征粒度上的并行。预先对特征进行排序，保存为 block 结构，后面可以重复使用（并行计算特征的信息增益），大大提升了计算的速度
  • XGBoost 使用（可并行的）近似特征划分法对特征进行划分，GBDT 使用传统贪心算法


当样本数量、特征数量、树的棵数增加，GBDT 训练时长分别是线性增加的吗？

  • 当样本数量增加：不是，假设树的棵数不变，对于单棵决策树来说，样本数量的增加带来的主要是来源于特征排序时间的增加，排序的复杂度不是线性的，而是接近 O(Nlog(N))
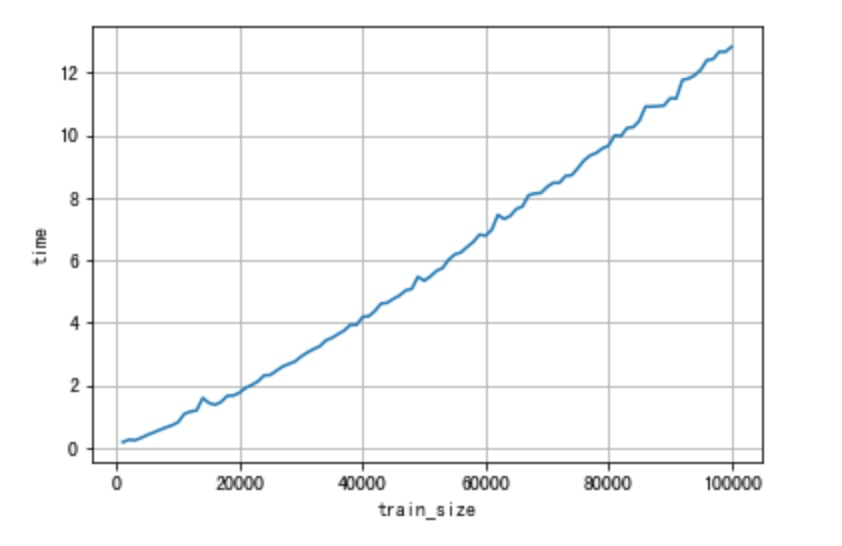
train_time_num_samples
  • 当特征数量增加：不考虑特征之间的性质差异，是的。特征数目的增加带来的训练时间的增加是线性的。
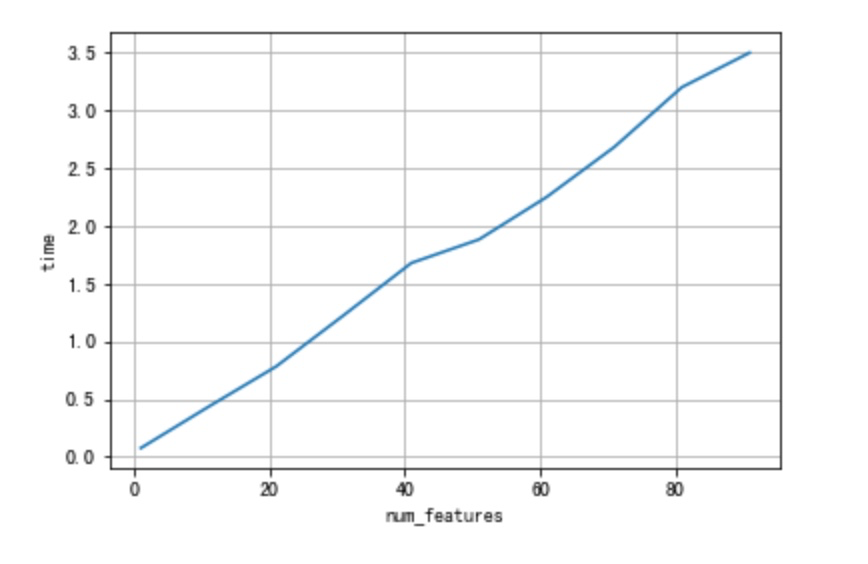
train_time_num_features
  • 当树的棵数增加：不考虑树的增加对模型收敛性的影响，是的。树的增加带来训练时间的增加是线性的。
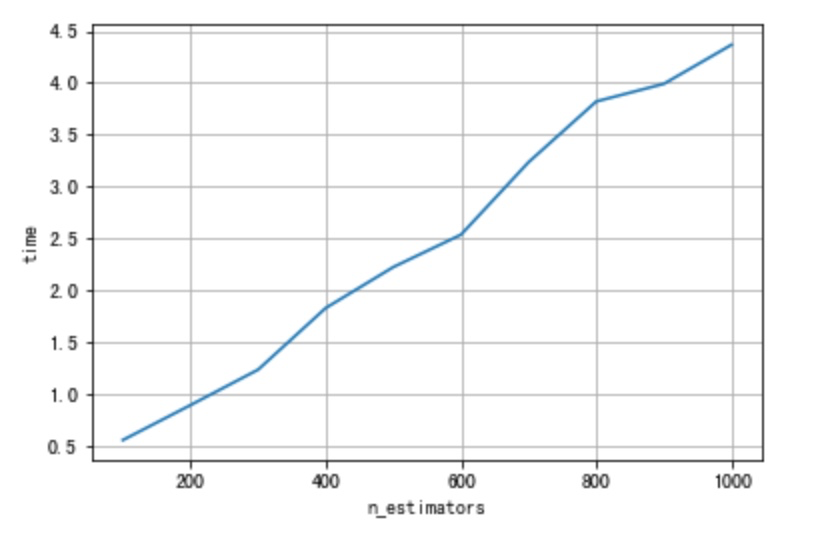
train_time_num_trees
  • 当树的最大深度增加：不是，树的最大深度线性增加带来的训练时间的增长是指数关系的。
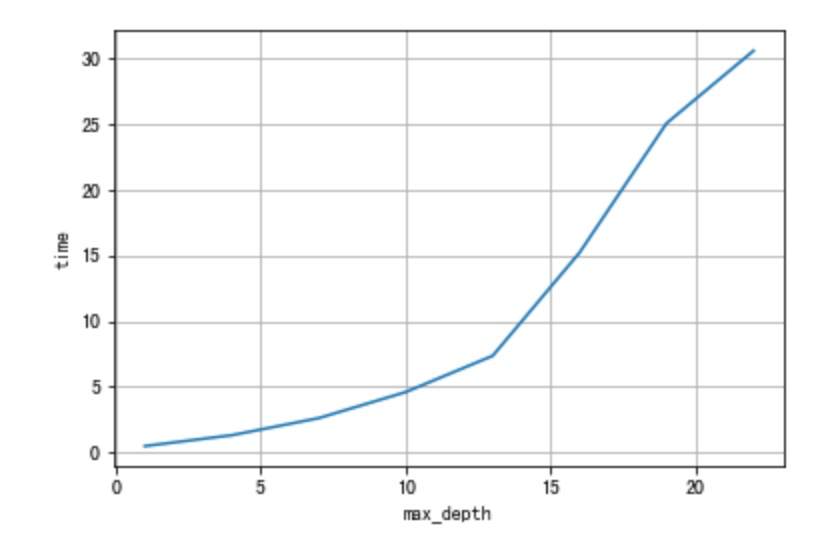
train_time_num_depths

详细代码见 这里


GBDT 中哪部分可以并行？

  • 计算每个样本损失函数的负梯度
  • 对特征进行排序、寻找最佳分裂点
  • 更新每样的负梯度
  • inference 时样本在所有树上的结果累加


杂七杂八

贝叶斯观点和频率观点有什么不同？

频率观点试图从「事件」出发，为事件本身建模，事件在独立重复事件中频率趋向于 p，则 p 就是事件的概率。

贝叶斯观点相反是从「观察者」角度出发，认为观察者知识不完备。在贝叶斯框架下，同一件事情，对于知情者而言是确定事件，对于不知情者是随机事件。即随机性并不是由事件本身决定，而是由观察者的知识状态决定。

贝叶斯推断试图描述观察者知识状态在新的观测后如何更新。假设观察者对某件事处于某种知识状态中（前置信念 prior belief），之后观察者开始新的观测，获得一些新的观测结果（evidence），通过满足一定条件的推断得出该陈述的合理性（likelihood），从而得出后置信念（posterior belief）来表征观测后的知识状态。


生成模型和判定模型的区别？

给定数据\(X\)，求解\(Y\) (类别或者连续值)，我们感兴趣的是条件概率\(P(Y|X)\)，有两种方法得到\(P(Y|X)\)：

  • 生成方法 generative method 生成方法对联合概率\(P(X,Y)\)进行建模。常见的生成方法有朴素贝叶斯，混合高斯模型等。使用生成方法的模型称为生成模型。 以朴素贝叶斯为例子，从样本中可以求得\(P(Y),P(X|Y)\)，进而得到联合分布\(P(X,Y)\)，再根据\(P(Y|X)=P(X,Y)P(Y)\)得到最终想要的\(P(Y|X)\)。

  • 判别方法 discriminative method 相比生成方法对\(P(X,Y)\)进行建模，判别方法直接对\(P(Y|X)\)进行建模。常见的判定模型有 LR、SVM、决策树等。 以 LR 为例子，LR 本质上是把\(P(Y|X)\)建模为：

$$P(Y|X)=\frac{1}{1 + exp(-(wx+b))}$$

生成模型其实包含了判别模型，因为我们总能由联合概率分布\(P(X,Y)\)得到\(P(Y|X)\)，这从侧面表明训练生成模型可能更加 expensive。 另外我们可以通过生成模型合成数据，但是没办法通过判别模型合成数据。

总结：生成模型对联合概率进行建模，而判别模型直接对条件概率进行建模。


L1 正则化为什么能让特征稀疏？

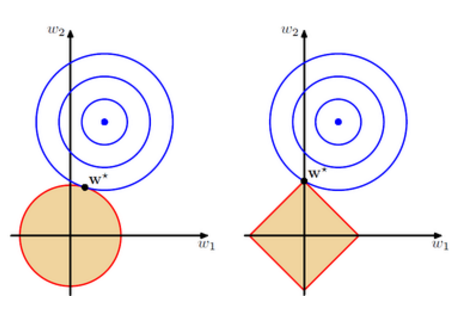
假设只有两个特征\(w_1, w_2\)，在损失函数中加入正则项相当于给解空间限制了条件。在下图中我们用橘色区域表示正则项的限制，蓝色等高线表示原损失函数对应的解。对于 L1，限定条件为：

$$|w_1|+|w_2|<some\ value$$

这个区域画出来如右下图橘色区域，蓝色点表示没有正则下的最优解，蓝圈表示次优解，我们需要寻找圈圈与橘黄色区域的交点。从图中可以看出，L1 正则化很大几率会与四个顶点相交（w1 或 w2 变为 0）。而对于 L2，限定条件为：

$$||w_1||^2 + ||w_2||^2 < some\ value$$

画出来如左下图橘色区域。除非最优解刚好处于坐标轴上，否则得到的解只会使参数变小，不会变为 0。

l1&l2


DNN 的特点？

主要有三点：

  1. 逐层堆叠的方式非常有利于表征学习（提取高级特征）。这个也是深度网络总体上比扁平网络效果好的原因。
  2. 特征的内部变换。这个是决策树以及基于决策树的 Boosting、Bagging 模型不具备的，他们始终是基于原始的特征空间，没有进行自动化的特征变换。
  3. 具备足够的模型复杂度，可以拟合复杂的非线性关系。