Support Vector Machine

本文对支持向量机（Support Vector Machine, SVM）进行数学推导。首先推导线性硬间隔 SVM，进一步引入 kernel trick 的非线性 SVM，再引入松弛变量的软间隔 SVM。最后整理关于 SVM 常见问题的笔记。

线性可分（硬间隔）SVM

SVM 基本思路就是在特征空间找到一个使间隔最大化的超平面。首先定义超平面为

$$ w^Tx+b=0 $$

其中$w, b$为模型参数，$x$为模型输入。

令$f(x)=w^Tx+b$，则

$$ f(x)=0 \qquad x 在平面上 $$ $$ f(x)<0 \qquad x 在平面一侧（负例） $$ $$ f(x)>0 \qquad x 在平面一侧（正例） $$

令 $y=+1$ 代表正样本， $y=-1$ 代表负样本。函数间隔 $\hat{\gamma}$ 可以表示为：

$$ \hat{\gamma}=yf(x)=y(w^Tx+b) $$

易得 $\hat{\gamma}$ 为非负。如果直接最大化函数间隔是有问题的，因为只要等比例地放大 $w,b$，就可以使函数间隔值任意大，但实际上超平面并没有变化。因此我们对函数间隔进行 scaling：

$$ \gamma=\frac{\hat{\gamma}}{\|w\|} $$

得到的 $\gamma$ 称为几何间隔，几何间隔不受 $w,b$ 等比缩放的影响。因此问题转化成对于所有训练样本，找到一组参数$w,b$ ，使得几何间隔$\gamma$ 最大。要最大化 $\gamma$ ，我们固定　$\hat{\gamma}$ 为１，即转变成最大化　$\frac{1}{\|w\|}$ ，等价于最小化　$\frac{1}{2}\|w\|^2$ （为了方便后续计算）。因此问题现在转变为：

$$ \text{minimize}_{w} \frac{1}{2}\|w\|^2 \quad s.t.\ y_i(w^Tx+b)\geq1,\forall i=1,...,N $$

这是一个带约束条件的二次线性优化问题，可以使用拉格朗日乘子将目标函数和约束条件融合：

$$ L(w,b,\alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^{N}\alpha_i \left( y_i(w^Tx_i+b)-1 \right) $$

其中 $\alpha\geq0$

令：

$$ \theta(w)=\text{maximize}_{\alpha\geq0}L(w,b,\alpha) $$

由于 $\alpha\geq0$ ，因此最大化 L 的最优解必然使 L 的第二项为 0，即

$$ \theta(w)=\frac{1}{2}\|w\|^2 $$

代回上面的问题表达式，将问题转化为：

$$ \text{minimize}_{w}\ (\text{maximize}_{\alpha\geq0}L(w,b,\alpha))$$ $$ s.t.\ y_i(w^Tx+b)\geq1, \alpha_i\geq0 \quad \forall i=1,...,N $$

该问题的对偶问题如下：

$$ \text{maximize}_{\alpha\geq0}\ (\text{minimize}_{w}L(w,b,\alpha))$$ $$ s.t.\ y_i(w^Tx+b)\geq1, \alpha_i\geq0 \quad i=1,...,N $$

记原问题的最优解为 $p^*$，对偶问题的最优解为 $d^*$，则有 $d^* \leq p^*$。更近一步，由于问题满足KKT 条件，其充分必要条件是$d^* = p^*$，因此求解原问题可以转化为求解对偶问题。接下来求解括号里的 $L(w,b,\alpha)$ 关于 $w,b$的最小值，分别令 $w,b$ 偏导等于 0 可以得到：

$$ w=\sum_{i=1}^{N}\alpha_iy_ix_i $$ $$ \sum_{i=1}^{N}\alpha_iy_i=0 $$

待回 $L(w,b,\alpha)$得到（消去 $w,b$）

$$ L(w,b,\alpha)=\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j {x_i}^T x_j $$

代入对偶问题中，得到我们最后的求解问题形式为：

$$ \text{maximize}_{\alpha\geq0}\ \sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j \langle x_i, x_j\rangle $$ $$ s.t.\ \sum_{i=1}^{N}\alpha_iy_i=0, \alpha_i\geq0 \quad \forall i=1,...,N $$

上式就是最终问题的形式，只要求出 $\alpha$ ，即可得到分类函数

$$ f(x)=w^Tx+b=\sum_{i=1}^{N}\alpha_i y_i\langle x_i,\boldsymbol x\rangle+b $$

计算出 $\alpha$后，我们就得到分类超平面，分类时只需计算输入 x 与少量支持向量的内积即可（非支持向量对应的 $\alpha$均为 0）。这就是最简单的线性可分（硬间隔）SVM 。

非线性 SVM（Kernel Trick）

前面关注的是数据在特征空间线性可分的情况，对于线性不可分的情况，我们可以把数据映射到更高维的空间中，使得数据在高维空间中线性可分。原先的分类函数如下：

$$ f(x)=w^Tx+b=\sum_{i=1}^{N}\alpha_i y_i\langle x_i,\boldsymbol x\rangle+b $$

令映射函数为 $\phi$，映射后分类函数为：

$$ f(x)=w^Tx+b=\sum_{i=1}^{N}\alpha_i y_i\langle \phi(x_i),\phi(\boldsymbol x)\rangle+b $$

如果只是简单的映射到高维空间，并计算高维空间向量的内积，有可能出现映射后维度太高，计算量太大的问题。核方法真正 tricky 的地方是，利用核函数直接在低维空间求解向量内积 $\langle x_i, x_j\rangle$ 得到高维空间的向量内积 $\langle \phi(x_i), \phi(x_j)\rangle$（而不是直接在高维空间计算）。比如下面这个核函数

$$ \kappa(x_1,x_2)=(\langle x_1,x_2\rangle)^2 $$

可以通过计算$\langle x_i, x_j\rangle$得到更加高维的$\kappa(x_1,x_2)$。将原空间的向量内积转换成核函数后，得到

$$ f(x)=w^Tx+b=\sum_{i=1}^{N}\alpha_i y_i\kappa(x_i,\boldsymbol x)+b $$

其中 $\alpha$由下列式子得到

$$ \text{maximize}_{\alpha\geq0}\ [\sum_{i=1}^{N}\alpha_i-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j \kappa(x_i, x_j)] $$ $$ s.t.\ \sum_{i=1}^{N}\alpha_iy_i=0, \alpha_i\geq0 \quad \forall i=1,...,N $$

在实际中，我们只关心经过映射数据线性可分，并不需要知道具体是什么映射，因此可是直接使用核函数计算低维内积得到映射后的高维内积(which is very nice)。

常用的核函数主要有三种：

多项式核（上面的例子就是一种多项式核

$$ \kappa(x_1,x_2)=(\langle x_1,x_2\rangle + R)^d $$

高斯核(RBF)

$$ \kappa(x_1,x_2)=exp(-\frac{\|x_1-x_2\|^2}{2\sigma^2})$$

线性核（相当于没有映射）

$$ \kappa(x_1,x_2)=\langle x_1,x_2 \rangle$$

实际应用中高斯核和线性核用的比较多，高斯核是最重要的一个核函数，主要参数是公式里面的 $\sigma$。$\sigma$越小，映射维度越高，理论上$\sigma$无穷小时高斯核可以映射到无限高维。

以上，引入了核函数的 SVM 成为非线性（软间隔）SVM。

软间隔 SVM（outlier）

实际中可能存在这样一种情况，即大部分数据是线性可分的，但存在一小部分噪音数据使得数据不能严格线性可分，即整体近似线性可分。虽然可以映射到高维空间变成线性可分的，但是因为可能实际数据分布在低维就是线性可分的。映射到高维后模型的容量可能大于问题本身的复杂程度，导致过拟合。对于少数偏离正常位置较远的异常点我们称为 outliers，如果使用之前的硬间隔 SVM，那么超平面会严重受到 outliers 的影响。我们通过允许一部分数据点在一定程度偏离超平面来解决这个问题。具体是将原来的约束条件变为：

$$ y_i(w^Tx+b)\geq1-\xi_i, \forall i=1,...,N $$

其中 $\xi$ 为松弛变量（slack variable），表示 $\xi_i$ 对应数据点 $x_i$ 允许偏离函数间隔的量。

同时在原来的目标函数中加入一项，使得 $\xi$ 的总和尽量小：

$$ \text{minimize}_{w,\xi} \frac{1}{2}\|w\|^2+C\sum_{i=1}^{N}\xi_i $$

其中 $C$ 是平衡“找到最大 margin”和“保证数据偏离总量最小”的参数。于是问题转化为：

$$ \text{minimize}_{w,\xi}\ \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{N}\xi_i$$ $$ s.t.\ \xi_i\geq0,y_i(w^Tx+b)\geq1-\xi_i \quad \forall i=1,...,N $$

按照上面的步骤得到最终需要求解的问题为：

唯一的区别就是 $\alpha$ 的取值多了一个上界 $C$

以上，针对数据近似线性可分情况，引入松弛你变量，得到软间隔 SVM。

SMO 算法

得到包含核函数和松弛变量的 SVM 模型后，最后就只需要对目标函数求解 $\alpha$。当前比较常用的方法是序列最小最优(SMO)算法。

SMO 算法的基本思路如下：迭代将原二次规划问题分解为只有两个变量的二次规划子问题，并对子问题进行解析求解，直至所有变量都满足条件为止。即每次选取两个$\alpha$，固定其他$\alpha$，针对这两个$\alpha$进行优化，使得优化之后模型（向着全局最优）提升最多。

SVM 损失函数

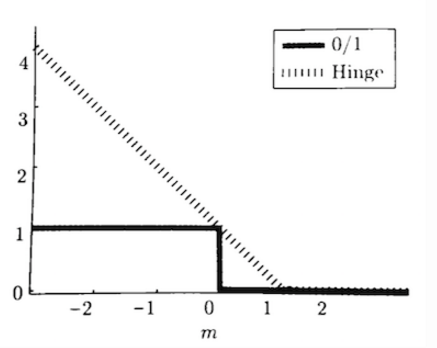
SVM 是一个二分类模型，二分类的一种损失函数是 0-1 损失（正例损失为 0，负例损失为 1），但是 0-1 损失难以直接优化，不是处处可微，因此 SVM 采用的是 hinge 损失。hinge 损失是 0-1 损失的一种近似，其表达式为：

$$ J_hinge(m)=\max\{0,1-m\} $$

0-1 损失和 hinge 损失的函数图像如下

上文的推导中好像并没有出现 hinge 损失的形式，为什么说 SVM 是采用 hinge 损失呢，我们回到软间隔 SVM 的损失函数

$$ \text{minimize}_{w,\xi} \ \frac{1}{2}\|w\|^2+C\sum_{i=1}^{N}\xi_i $$ $$ s.t.\ \xi_i\geq0,y_i(w^Tx+b)\geq1-\xi_i \quad \forall i =1,...,N $$

上式可以改写成以下形式：

$$ \text{minimize}_{w,\xi} \ C\sum_{i=1}^{N}\max \{0, 1-y(w^Tx+b)\}+\frac{1}{2}\|w\|^2$$

上式第一项其实就是 hinge 损失的形式。

如果 $1-y(w^Tx+b)<0$，则该点不是越界点，loss 第一项为 0；
如果 $1-y(w^Tx+b)>0$ ，则该点是越界点，loss 为 $1-y(w^Tx+b)$；

上式第二项可以看做是 L2 正则化损失。因此优化 SVM 损失函数可以看做优化 hinge 损失+ L2 正则化。

Q & A

SVM 为什么采用间隔最大化？

因为当数据线性可分时是存在无数个朝平面可以正确分类的，感知机采用误分类点到超平面距离最小策略，而 SVM 采用间隔最大化解得超平面，具有更好的鲁棒性和泛化能力。
原问题和对偶问题分别是什么？为什么要转化成为对偶问题？

通过求解原问题我们可以直接获得最优的 $w$，但并不清楚 $\alpha$ 的取值情况，在给定一个样本点 $x$ 进行分类时，我们需要计算 $w^T x+b$ ，这在 $w$ 的维度比较大时计算量是比较大的。而求解对偶问题则是对 $\alpha$ 进行求解，最后分类时计算 $w^Tx+b=\sum_{i=1}^{N}\alpha_i y_i\langle x_i,\boldsymbol x\rangle+b$ ，由于$\alpha$ 对于非支持向量都为 0，因此计算量可以大大减少，并且可以使用核技巧维度变换。

总结来说，原问题的算法复杂度和样本维度 $w$ 有关，对偶问题的算法复杂度和样本数量（拉格朗日算子 $\alpha$ ）有关。在维度小样本多的情况下直接在原问题下求解就行了（线性分类经常出现的情况），但是对于非线性分类，通常经过核技巧升维后维度会大于样本数量，这种情况下求解对偶问题更方便。
为什么要引进核函数？

当样本线性不可分时，可以通过将样本映射到更高维的空间，使得样本在高维空间线性可分。而核函数就是计算高维空间向量内积的函数。即核函数虽然也是将低维向量映射到高维空间，但是他并不需要确定的映射函数，而是直接使用低维空间的内积计算映射过后的内积。
加大数据量一定能提高 SVM 准确率吗？
- 加大数据量提升准确率这一做法是在模型出现了 Overfitting 的情况下才有可能出现。uUnferfitting 时，比如数据是线性不可分的，而使用了线性 SVM，此时加大数据量不会有任何提升。
- 在模型复杂度和问题复杂度相当的前提下，加大数据量是会有一定的提升的。
- 最后还需要考虑数据的质量，如果增加夹杂太多噪声数据可能反而使准确率下降。
SVM practical skills
- 核的选择
  
  一般情况下 RBF 是第一选择，线性核是 RBF 核的一种特殊情况，sigmoid 核在某些参数下和 RBF 和类似。RBF 和比多项式核拥有更少的参数。
  1. 如果 feature 的数量很大（跟样本数量差不多），选用线性核；
  2. 如果 feature 的数量比较小，样本数量不算大也不算小，选用 RBF；
  3. 如果 feature 的数量比较小，而样本数量很多，则手工添加一些 feature 变成第一种情况；
- RBF 核参数的设置
  
  RBF 核重要的参数有两个，一个是惩罚系数 C，另一个是高斯核中的 sigma。
  1. C 可以理解为正则化系数。
    - 当 C 大时，损失函数也会比较大，即对离群点的惩罚程度大，选择支持向量的时候会更多的考虑这些离群点，使得支持向量变多，模型复杂；
    - 当 C 小时，对离群点的惩罚程度小，即不太重视那些离群点，最终支持向量会比较少，模型比较简单；
  2. $\sigma$ 可以理解为控制映射维度的参数
    - 当$\sigma$ 很大时，支持向量越少，相当于映射到一个低维空间，平滑效应太大；
    - 当$\sigma$ 很小时，支持向量很多，可以映射到高维空间，理论上当$\sigma$无穷小是可以拟合任何非线性数据，但是容易过拟合。
- Scaling
  
  SVM 是基于距离的模型，对距离的表示比较敏感。因此在应用 SVM 之前要对数据进行 scaling，对 training set 和 test set 要用同样的方法 scaling。
KKT 条件

对于一个带不等式约束的优化问题：

$$ f(x), s.t.\ g_i(x)\leq0;h_j(x)=0 \ \forall i,j =1,...,N $$

写成拉格朗日乘子问题：

$$ L(\alpha,\beta,x)=f(x)+\alpha g(x)+\beta h(x) $$

最优值满足下面条件(KKT 条件)：

$$ \frac{\partial L(\alpha,\beta,x)}{\partial x}=0 $$ $$ \alpha g(x)=0 $$ $$ h(x) = 0 $$

KKT 条件是拉格朗日乘子法的泛化，适用于约束条件是包含不等式约束的情况（一般二次优化就求导令导数为 0，带等式约束的就使用拉格朗日乘子法，带不等式约束并且满足 KKT 条件就使用 KKT 算法，SVM 的问题满足 KKT 条件）。

KKT 条件是强对偶条件的必要条件，即满足 KKT 条件就满足强对偶条件。因此 min_max something 的最优解等于 max_min_something 的最优解。SVM 就利用强对偶性进行了转换求解。

关于 KKT 条件参考：这里

Guibo Wang