Gradient Boosting

本文主要是记下在学习 Gradient Boosting 算法过程中的一些推导、笔记和思考。

概要

Boosting 是集成学习中非常重要的一类算法，其基本原理是串行生成一系列弱学习器（weak learner），这些弱学习器直接通过组合到一起构成最终的模型。Boosting 算法可以用于解决分类和回归问题，主要的算法包括 AdaBoost 和 Gradient Boosting。本文主要关注 Gradient Boosting，以及相关的 GBDT 和 XGBoost。AdaBoost 本质上也可以从广义的 Gradient Boosting 推导得到（损失函数使用指数损失），这里不详细展开，详细的推导见 MLAPP 第 16.4.3 节。

Gradient Boosting 基本思想

Gradient Boosting 的基本思想是：串行地生成多个弱学习器，每个弱学习器的目标是拟合先前累加模型的损失函数的负梯度， 使加上该弱学习器后的累积模型损失往负梯度的方向减少。

举个简单的例子，假设有个样本真实值为 10，第一个若学习器拟合结果为 7，则残差为 10-7=3；则残差 3 作为下一个学习器的拟合目标，第二个若学习其拟合结果为 2，则这两个弱学习器组合而成的 Boosting 模型对于样本的预测为 7 + 2 = 9，以此类推可以继续增加弱学习器以提高性能。这只是一个非常非常简单的例子，但这也就是 Gradient Boosting 的基本思想了。

Gradient Boosting 还可以将其理解为函数空间上的梯度下降。我们比较熟悉的梯度下降通常是值在参数空间上的梯度下降（如训练神经网络，每轮迭代中计算当前损失关于参数的梯度，对参数进行更新）。而在 Gradient Boosting 中，每轮迭代生成一个弱学习器，这个弱学习器拟合损失函数关于之前累积模型的梯度，然后将这个弱学习器加入累积模型中，逐渐降低累积模型的损失。即 参数空间的梯度下降利用梯度信息调整参数降低损失，函数空间的梯度下降利用梯度拟合一个新的函数降低损失。

公式推导

假设有训练样本 $\{x_i, y_i\}, i=1...n$ ，在第 m-1 轮获得的累积模型为 $F_{m-1}(x)$，则第 m 轮的弱学习器 $h(x)$ 可以通过下式得到

$$ F_m(x) = F_{m-1}(x) + \mathop{\arg\min}_{h \in H}Loss(y_i, F_{m-1}(x_i) + h(x_i)) $$

上式等号右边第二项的意思是：在函数空间 $H$ 中找到一个弱学习器 $h(x)$，使得加入这个弱学习器之后的累积模型的 loss 最小。那么应该如何找这个 $h(x)$ 呢？在第 m-1 轮结束后，我们可以计算得到损失 $Loss(y, F_{m-1}(x))$，如果我们希望加入第 m 轮的弱学习器后模型的 loss 最小，根据最速下降法新加入的模型应该损失函数应该沿着负梯度的方向移动，即如果第 m 轮弱学习器拟合损失函数关于累积模型$F_{m-1}(x)$ 的负梯度，则加上该弱学习器之后累积模型的 loss 会最小。

因此可以得知第 m 轮弱学习器训练的目标值是损失函数的负梯度，即

$$ g_m=-\frac{\partial Loss(y, F_{m-1}(x))}{\partial F_{m-1}(x)} $$

如果 Gradient Boosting 中采用平方损失函数 $Loss=(y - F_{m-1}(x))^2$，损失函数负梯度计算出来刚好是残差 $y - F_{m-1}(x)$，因此有些资料也会说 Gradient Boosting 每一个弱学习器是在拟合之前累积模型的残差。但这样的说法不具有一般性，如果使用其他损失函数或者在损失函数中加入正则项，那么负梯度就不再刚好是残差。

由此可以得到完整的 Gradient Boosting 算法流程：

Algorithm: Gradient Boosting

Initialize $F_0(x) = \mathop{\arg\min}_{h \in H}Loss(y_i, h(x_i))$
For m=1:M Do:
- Compute the negative gradient $g_m = -\frac{\partial Loss(y, F_{m-1}(x))}{\partial F_{m-1}(x)}$
- Fit a weak learner which minimize $\sum_{i=1}^{N}(g_m^i - h(x_i))^2$
- Update $F_m = F_{m-1} + vh(x)$
Return $F(x) = F_M(x)$

以上 Gradient Boosting 的算法流程具有一般性，根据其中的损失函数和弱学习器的不同可以演变出多种不同的算法。如果损失函数换成平方损失，则算法变成 L2Boosting；如果将损失函数换成 log-loss，则算法成为 BinomialBoost；如果是指数损失，则算法演变成 AdaBoost；还可以采用 Huber loss 等更加 robust 的损失函数。弱学习器如果使用决策树，则算法成为 GBDT（Gradient Boosting Decision Tree）。使用使用决策树作为弱学习器的 GBDT 使用较为普遍，接下来两节对 GBDT 进行介绍。

GBDT 回归与分类

GBDT（Gradient Boosting Decision Tree）是弱学习器使用 CART 回归树的一种 Gradient Boosting，使用决策树作为弱学习器的一个好处是：决策树本身是一种不稳定的学习器（训练数据的一点波动可能给结果带来较大的影响），从统计学的角度单棵决策树的方差比较大。而在集成学习中，弱学习器间方差越大，弱学习器本身泛化性能越好，则集成学习模型的泛化性能就越好。因此使用决策树作为弱学习器通常比使用较稳定的弱学习器（如线性回归等）泛化性能更好。

回归问题

GBDT 中的每个弱学习器都是 CART 回归树，在回归问题中，损失函数采用均方损失函数：

$$ Loss(y, F_{m-1}(x))=(y - F_{m-1}(x))^2 $$

损失函数的负梯度为：

$$ g_m = y - F_{m-1}(x)$$

代入 Algorithm1 中可以得到 GBDT 回归的流程。核心代码如下：

def fit(self, train_X, train_y):
    self.estimator_list = list()
    self.F = np.zeros_like(train_y, dtype=float)

    for i in range(1, self.n_estimators + 1):
        # get negative gradients
        neg_grads = train_y - self.F
        base = DecisionTreeRegressor(max_depth=self.max_depth)
        base.fit(train_X, neg_grads)
        train_preds = base.predict(train_X)
        self.estimator_list.append(base)

        if self.is_first:
            self.F = train_preds
            self.is_first = False
        else:
            self.F += self.lr * train_preds

上述代码中 2、3 行是初始化工作，从第 5 行开始循环逐个生成弱学习器。循环体内首先计算负梯度，然后使用弱学习器拟合负梯度，这里偷懒直接调用了 sklearn 的 DecisionTreeRegressor 作为 weak learner :)，然后将当前弱学习器的预测累加到 F 中，保存该弱学习器，进入下一轮的循环。

模型超参数设定为 n_estimators 为 300， max_depth 为 5，lr 为 0.1，数据集选用 BlackFridy，这个数据集总共有 11 维特征，537577 条数据，按照 0.8/0.2 随机划分训练集和验证集。首先我们拿这个模型与 sklearn 的 GradientBoostingRegressor 进行对比如下，可以看到结果差不多。

GradientBoostingRegressor train_score: 0.7106 valid_score: 0.7037
MyGradientBoostingRegressor train_score: 0.7121 valid_score: 0.7054

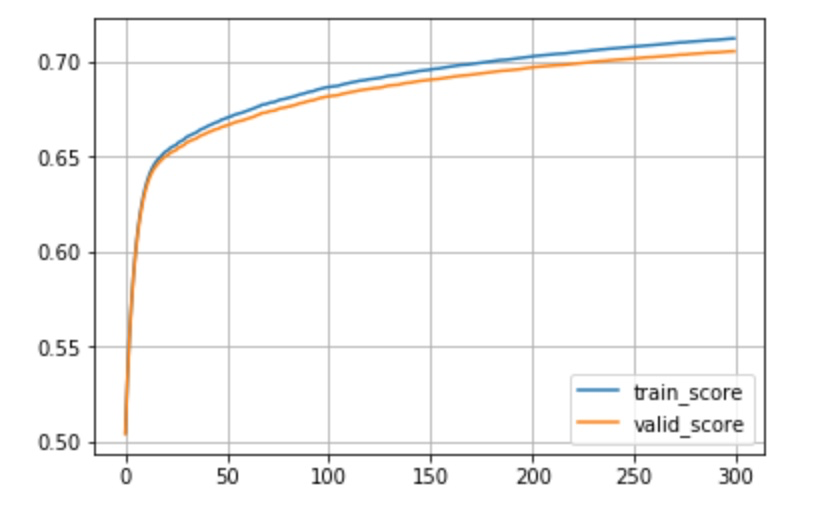
把训练过程的 train_score 和 valid_score 画出来，可以看到随着决策树棵数增多，train_score 在不断提高，valid_score 也在同步提升。由于训练数据量比较大，在当前模型容量下模型还不会出现过拟合，train_score 增高 valid_score 也在随之增高。

分类问题

GBDT 中都的弱学习器都是 CART 回归树，在回归问题上使用 GBDT 比较 intuitive，损失函数为均方损失，负梯度就是残差，下一棵树就去拟合之前的树的和与真实值的残差。对于分类问题，可以对拟合目标稍作转换实现分类。

基本的思路可以参考线性回归通过对数几率转化为逻辑回归进行分类。逻辑回归也是广义上的线性模型，可以看做是线性回归模型 $wx + b$ 去拟合对数几率 $\mathop{\log}\frac{p}{1-p}$：

$$ wx + b = \mathop{\log}\frac{p}{1-p} $$

损失函数是交叉熵损失：

$$ Loss = -y\mathop{\log}p - (1-y)\mathop{\log}(1-p) $$

在 GBDT 中可以看做是前 m-1 轮的累积模型 $F_{m-1}$ 代替了线性模型 $wx + b$ 去拟合对数几率，令

$$ F_{m-1} = \mathop{\log}\frac{p_{m-1}}{1-p_{m-1}} $$

有

$$ p_{m-1} = \frac{1}{1+\mathop{\exp}(-F_{m-1})} $$

代入交叉熵损失中得到

$$ Loss = \mathop{\log}(\mathop{\exp}(F_{m-1}) + 1) - yF_{m-1}$$

对损失函数求偏导得负梯度

$$ -\frac{\partial Loss}{\partial F_{m-1}} = y - p_{m-1} $$

可以看到最后的负梯度形式十分简洁，将此负梯度作为第 m 轮的拟合目标，依次不断迭代，GBDT 分类的核心代码如下：

@staticmethod
def logit(F):
    return 1.0 / (1.0 + np.exp(-F))

def fit(self, train_X, train_y):
    self.estimator_list = list()
    self.F = np.zeros_like(train_y, dtype=float)

    for i in range(1, self.n_estimators + 1):
        # get negative gradients
        neg_grads = train_y - self.logit(self.F)
        base = DecisionTreeRegressor(max_depth=self.max_depth)
        base.fit(train_X, neg_grads)
        train_preds = base.predict(train_X)
        self.estimator_list.append(base)

        if self.is_first:
            self.F = train_preds
            self.is_first = False
        else:
            self.F += self.lr * train_preds

在 heart-disease-uci 数据集中分类的准确率为

GradientBoostingRegressor train_score: 0.9834 valid_score: 0.7705
MyGradientBoostingRegressor train_score: 0.7171 valid_score: 0.8361

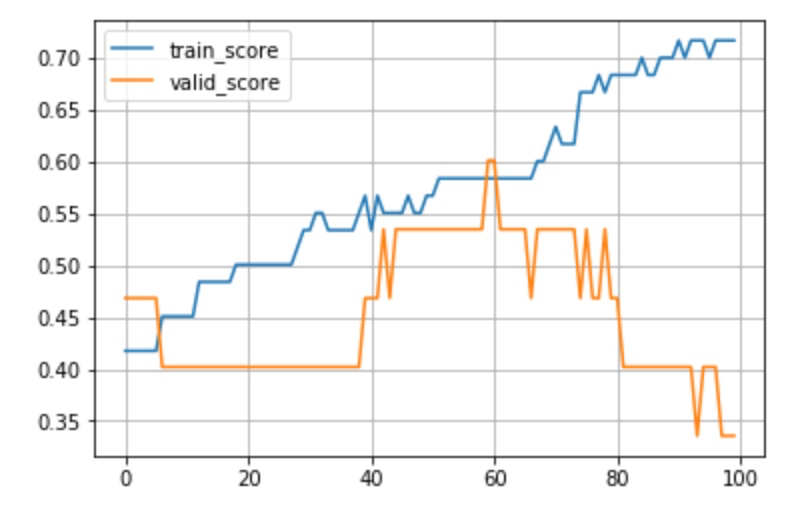
训练过程的 train_score 和 valid_score 如下图，可以看到随着决策树棵数增多，训练集的 score 在都不断提高，而 valid_score 在 60 轮左右达到 0.6 之后就开始下降，出现了明显的过拟合。这里是由于采用的这个数据集数据量比较小，训练集和验证集分别只有 242 和 61 条数据。

以上的 GBDT 分类和回归的完整代码可以在这里找到。

GBDT 优点和局限性

优点

预测阶段速度快，树与树之间可以并行预测
在数据分布稠密的数据上，泛化能力和表征能力都很好
使用 CART 作为弱分类器不需要对数据进行特殊的预处理如归一化等

局限性

在高维稀疏的数据上，表现不如 SVM 或神经网络
训练过程需要串行训练，只能在决策树内部采用一些局部并行手段提高训练速度

总结

本文对 Gradient Boosting 算法的思想、原理和推导进行了阐述，对以 CART 回归树作为弱学习器的 GBDT 分类和回归算法进行了介绍，并附上了简单的代码实验。在经典机器学习场景中，以 GBDT 为代表的 Gradient Boosting 算法效果优秀，得到了广泛的应用，是一类值得深入探索的经典机器学习算法。更多关于 Gradient Boosting 的内容，可以阅读 Greedy Function Approximation: A Gradient Boosting Machine, XGBoost: A Scalable Tree Boosting System 等经典 paper。

Guibo Wang